Avertissement
Ceci n'est pas un cours, ni sur les monoïdes, ni sur les groupes, la géométrie, les permutations ou tout autre chose. Ceci n'est qu'une compilation de quelques notions indispensables pour une meilleure connaissance des puzzles Rubik ou apparentés.
Monoïdes, Produits
Un monoïde est un ensemble dont les éléments sont des chaînes de caractères composées des lettres d'un alphabet.
Un monoïde doit posséder une opération de concaténation qui produit une seule chaîne de caractères à partir de deux chaînes de caractères.
Un monoïde doit aussi posséder au moins un élément neutre (c'est-à-dire qui n'a aucun effet) pour l'opération de concaténation de chaînes.
Le Rubik's Cube est un monoïde.
{A,P,G,D,H,B} est un alphabet de 6 lettres qui désigne les faces Avant, Postérieure, Gauche, Droite, Haut et Bas. En partant du cube initial n'importe quel cube peut être obtenu en composant une chaîne à partir de cet alphabet.
Concaténer deux chaînes de l'alphabet {A,P,G,D,H,B} revient à enchaîner deux mouvements.
Le cube possède au moins un élément neutre, par exemple la chaîne AAAA, que l'on peut aussi noter A⁴, qui consiste à effectuer un tour complet de la face Avant. A⁴ est un élément neutre pour la concaténation de chaînes puisqu'il ne perturbe pas la configuration du cube.
Groupes, Symétrie, Inverse
Un groupe est un monoïde qui possède une notion de symétrie.
Un groupe est muni d'une opération inverse, c'est-à-dire que pour chaque chaîne il existe une chaîne inverse qui rétabli l'état de départ.
Le Rubik's Cube est un groupe.
Les inverses de A,P,G,D,H,B sont (respectivement) AAA,PPP,GGG,DDD,HHH,BBB que l'on peut aussi noter (respectivement) A³,P³,G³,D³,H³,B³
L'inverse d'une chaîne U.V est la chaîne Vˉ¹.Uˉ¹
Schéma de couleurs standard
Sur un Rubik's Cube les couleurs ne sont pas réparties au hasard, le schéma de couleur est standardisé.
Placez votre cube comme ceci :
Effectuez ce mouvement :
Vous devez obtenir ceci :
Dans le cas contraire achetez un ensemble d'autocollants ou bien un autre cube qui respecte le standard de couleurs.
La règle mnémotechnique c'est que la couleur de la face opposée ajoute la composante jaune :
- jaune s'oppose à blanc
- orange s'oppose à rouge
- vert s'oppose à bleu
Géométrie, Repère, Perspective cavalière
Le cube est un solide platonique qui possède :
- 8 coins
- 12 arêtes
- 6 faces
- 24 symétrie non chirales, c'est-à-dire qu'un cube possède 24 façons de vous présenter 3 faces visibles
Une façon traditionnelle de présenter les 3 faces visibles est de le faire à l'aide d'une perspectives cavalière. De cette façon les faces sont clairement désignées :
- la face Avant est celle qui apparaît comme un carré
- les faces Droite et Haut apparaissent comme un parallélogramme
- les faces Postérieure, Gauche et Bas sont (respectivement) les faces opposées
Un Rubik's Cube possède 3 types de pièces :
- 8 pièces-coins qui portent 3 étiquettes de couleur distinctes
- des pièces-arêtes qui portent 2 étiquettes de couleur distinctes
- des pièces-centres qui ne portent qu'une seule étiquette
Il est possible d'identifier une des 12 arêtes en la désignant comme l'intersection de deux faces. Par exemple l'arête AD est à l'intersection de la face Avant et de la face Droite.
Il est possible d'identifier un des 8 coins en le désignant comme l'intersection de trois faces. Par exemple le coin AHD est à l'Avant, en Haut à Droite.
Pictogrammes
Sauf quelques rares exceptions les pictogrammes indiquent le mouvement à appliquer tout en regardant la face Avant, celle qui est carrée dans la réprésentation isométrique du cube.
Les barres droites représentent les colonnes ou les rangées.
La flèche indique le sens de la rotation.
Quelques exemples sur un cube classique :
-
 effectuer un ¼ de tour, dans le sens horloge, sur la face Avant
effectuer un ¼ de tour, dans le sens horloge, sur la face Avant
-
 effectuer un ¼ de tour, dans le sens horloge, sur la face Droite
effectuer un ¼ de tour, dans le sens horloge, sur la face Droite
-
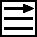 effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Haute
effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Haute
-
 effectuer un ¼ de tour sur la tranche médiane horizontale
effectuer un ¼ de tour sur la tranche médiane horizontale
-
 effectuer un ¼ de tour, dans le sens horloge, sur la face Postérieure
effectuer un ¼ de tour, dans le sens horloge, sur la face Postérieure
 la couleur rouge n'a pas d'importance, elle n'est là que pour figurer que la dernière colonne de Droite devient la première rangée de la face Haute
la couleur rouge n'a pas d'importance, elle n'est là que pour figurer que la dernière colonne de Droite devient la première rangée de la face Haute
-
 effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Postérieure
effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Postérieure
 la couleur rouge n'a pas d'importance, elle n'est là que pour figurer que la première rangée de la face Haute devient la dernière colonne de Droite
la couleur rouge n'a pas d'importance, elle n'est là que pour figurer que la première rangée de la face Haute devient la dernière colonne de Droite
La particularité des tours (ou parallélépipèdes) c'est que :
- les tranches horizontales sont carrées ce qui permet le ¼ de tour
- les tranches verticales sont rectangulaires ce qui ne permet que le ½ tour
Quelques exemples sur la tour 3² × 4 :
-
 effectuer un ¼ tour, dans le sens horloge, sur la moitié Haute
effectuer un ¼ tour, dans le sens horloge, sur la moitié Haute
-
 effectuer un ½ tour sur la face Avant
effectuer un ½ tour sur la face Avant
 cette face étant rectangulaire le ¼ de tour n'existe pas
cette face étant rectangulaire le ¼ de tour n'existe pas
-
 effectuer un ½ tour sur la face Droite
effectuer un ½ tour sur la face Droite
 car cette face est également rectangulaire
car cette face est également rectangulaire
-
 effectuer un ¼ tour, dans le sens horloge inverse, sur la face Bas
effectuer un ¼ tour, dans le sens horloge inverse, sur la face Bas
Résolu et non-résolu
Dans la permutation initiale aucune pièce et aucune étiquette n'est échangée avec une autre.
Un puzzle rubik est dit résolu quand il est dans la permutation initiale.
Une pièce est dite résolue quand elle est à la même place et dans la même orientation que dans la permutation initiale.
Placer
Placer c'est l'action de ramener une pièce à sa position initiale.
Cette position est déterminée relativement à des pièces fixes ou à d'autres pièces déjà placées.
Pour amener une pièce à sa position initiale il faut l'échanger avec au moins une autre pièce du même groupe.
C'est pourquoi il est impossible qu'une seule pièce d'un même groupe soit mal placée.
Sur l'image ci-dessous 3 arêtes sont mal placées, pour les placer correctement il faudrait les échanger dans le sens des aiguilles d'une montre.
Une pièce bien placée n'est pas tout à fait résolue si elle est encore mal orientée.
Orienter
Orienter c'est l'action de ramener une pièce dans son orientation initiale.
Pour orienter une pièce il faut opérer un échange sur ses étiquettes.
Sur l'image ci-dessous 2 arêtes sont mal orientées, pour les orienter correctement il faudrait échanger leurs étiquettes.
L'échange des étiquettes d'une pièce entraine un échange d'étiquettes sur au moins une autre pièce du même groupe.
C'est pourquoi il est impossible qu'une seule pièce d'un même groupe soit mal orientée.
Inverse
Le mouvement inverse d'une série de pictogrammes s'obtient :
- en lisant de droite-à-gauche au lieu de gauche-à-droite
- en inversant le sens des flèches
Sur toutes les tranches carrées ou rectangulaires, puisque le tour complet est un élément neutre, le ½ tour est toujours son propre inverse.
Commutativité
La commutativité c'est l'indifférence à l'ordre des opérations. La commutativité concerne n'importe quelle opération, même dans la vie quotidienne.
Par exemple :
- enfiler un bonnet, une écharpe et des gants en laine sont des opérations qui commutent, je peux les faire dans n'importe quel ordre et le résultat sera toujours le même
- enfiler les chaussettes ne commute pas avec enfiler les chaussures
- enfiler un sous-vêtement ne commute pas avec enfiler un sur-vêtement
- griller une allumette ne commute pas avec ouvrir le gaz
D'où une question d'importante capitale :
La résolution des centres, des coins et des arêtes commute-t-elle

La réponse est affirmative, les différents sortes de pièces se trouvent dans des groupes indépendants que l'on peut résoudre indépendamment, il n'y a pas d'ordre de résolution.
 Si je résous le cube couronne par couronne et non pas sorte de pièce par sorte de pièce, alors la commutativité n'a plus d'importance
Si je résous le cube couronne par couronne et non pas sorte de pièce par sorte de pièce, alors la commutativité n'a plus d'importance

Au contraire, la commutativité est universelle, pour résoudre le cube couronne par couronne il faudra :
- que la résolution des arêtes de la 2nd couronne laisse intacts les coins de la 1ère couronne
- que la résolution des arêtes de la 3ième couronne laisse intacts les coins de la 1ère et de la 2ième couronne.
- que la résolution des coins de la 3ième couronne laisse intactes les arêtes de la 1ère et de la 2ième couronne
Un graphe commutatif est un graphe où en partant de l'origine vous arrivez au même point d'arrivée quel que soit le chemin emprunté.
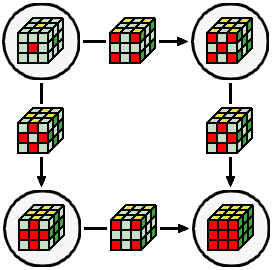
On peut résumer la commutativité coins-arêtes dans un graphe commutatif :
diagramme commutatif de la résolution du cube
Où :
- les flèches représentent les opérations qui résolvent les pièces de couleur vive tout en laissant intactes les pièces de couleur grise
- ces flèches ne sont pas des mouvements quelconques, on appelle ces mouvements des commutateurs, ils agissent uniquement sur un certain type de pièce et pas sur les autres
- les cercles représentent les ensembles où toutes les pièces de couleur vive sont résolues
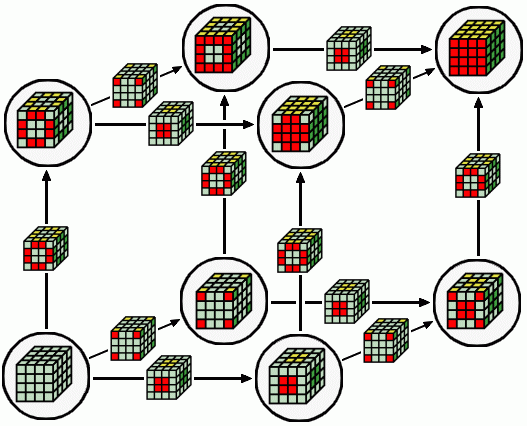
Dans un cube 4³ il y a une 3ième sorte de pièce à placer: les centres, ça ajoute une dimension supplémentaire au graphe commutatif.
diagramme commutatif de la résolution du 4³
Mouvements symétriques
Lorsque vous avez trouvé un mouvement vous avez également trouvé :
- son mouvement inverse
- ses mouvement symétriques ainsi que leurs inverses
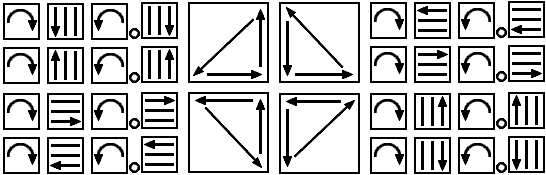
 les quatres mouvement ceci-dessus servent à échanger 3 coins d'une face
les quatres mouvement ceci-dessus servent à échanger 3 coins d'une face
 le point-rond
le point-rond
 ne sert qu'à la ponctuation, il aide à identifier le mouvement comme étant un commutateur de la forme B.A.Bˉ¹.Aˉ¹
ne sert qu'à la ponctuation, il aide à identifier le mouvement comme étant un commutateur de la forme B.A.Bˉ¹.Aˉ¹
En pratique il n'est pas très utile de connaître les mouvements symétriques, car il est beaucoup plus simple de pivoter manuellement le cube plutôt que de transformer mentalement un mouvement en son mouvement symétrique.
Commutateurs
La grosse difficulté du Rubik's Cube vient de ce qu'à un moment vous ne savez plus comment construire sans démolir ce que vous avez déjà obtenu. Pourquoi ?
Parce que vos actions ne commutent pas.
Si vos actions commutaient vous n'auriez aucun souci. Résoudre le cube deviendrait aussi facile qu'enfiler vos gants puis votre bonnet ou bien enfiler votre bonnet puis vos gants. Tout le jeu du Rubik's Cube consiste donc à construire des actions qui commutent les unes avec les autres. Ce paragraphe prend tout son sens quand vous vous reportez au
diagramme commutatif de la résolution du cube
.
Un commutateur est toujours un mouvement de la forme B.A.Bˉ¹.Aˉ¹
La réciproque est fausse, les mouvements de la forme B.A.Bˉ¹.Aˉ¹ ne sont pas tous des commutateurs.
Conjugaisons
Un commutateur est souvent donné comme une liste de pictogrammes qui conduit d'une position à une autre. En pratique la position de départ diffère souvent de celle de la formule. C'est pourquoi il est nécessaire d'avoir un moyen de dériver quantité de nouvelles formules à partir de la formule de base.
La conjugaison C d'un commutateur B.A.Bˉ¹.Aˉ¹ est le mouvement C.(B.A.Bˉ¹.Aˉ¹).Cˉ¹
Une conjugaison se fait donc en trois étapes :
- la première étape est C et consiste à se ramener à une position à partir de laquelle on sait appliquer le commutateur B.A.Bˉ¹.Aˉ¹
- la seconde étape consiste à appliquer le commutateur B.A.Bˉ¹.Aˉ¹
- la troisième étape consiste à se ramener en position initiale en appliquant Cˉ¹
 Version d'archive
Version d'archive



![[FACEBOOK] Les amis du travail bien fait [FACEBOOK] Les amis du travail bien fait](/var/crypte/storage/images/media/images/vignette/vignette-question/30275-1-fre-FR/Vignette-Question_vignette_article.png)











 effectuer un ¼ de tour, dans le sens horloge, sur la face Avant
effectuer un ¼ de tour, dans le sens horloge, sur la face Avant effectuer un ¼ de tour, dans le sens horloge, sur la face Droite
effectuer un ¼ de tour, dans le sens horloge, sur la face Droite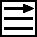 effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Haute
effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Haute effectuer un ¼ de tour sur la tranche médiane horizontale
effectuer un ¼ de tour sur la tranche médiane horizontale effectuer un ¼ de tour, dans le sens horloge, sur la face Postérieure
effectuer un ¼ de tour, dans le sens horloge, sur la face Postérieure
 la couleur rouge n'a pas d'importance, elle n'est là que pour figurer que la dernière colonne de Droite devient la première rangée de la face Haute
la couleur rouge n'a pas d'importance, elle n'est là que pour figurer que la dernière colonne de Droite devient la première rangée de la face Haute effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Postérieure
effectuer un ¼ de tour, dans le sens horloge inverse, sur la face Postérieure

 effectuer un ¼ tour, dans le sens horloge, sur la moitié Haute
effectuer un ¼ tour, dans le sens horloge, sur la moitié Haute effectuer un ½ tour sur la face Avant
effectuer un ½ tour sur la face Avant
 effectuer un ½ tour sur la face Droite
effectuer un ½ tour sur la face Droite
 effectuer un ¼ tour, dans le sens horloge inverse, sur la face Bas
effectuer un ¼ tour, dans le sens horloge inverse, sur la face Bas


 ne sert qu'à la ponctuation, il aide à identifier le mouvement comme étant un commutateur de la forme B.A.Bˉ¹.Aˉ¹
ne sert qu'à la ponctuation, il aide à identifier le mouvement comme étant un commutateur de la forme B.A.Bˉ¹.Aˉ¹