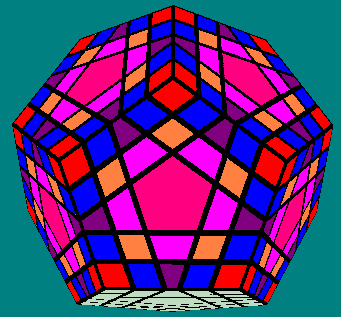|
|
 Posté
il y a plus de 16 ans
, modifié
il y a plus de 15 ans
par Ertaï
Posté
il y a plus de 16 ans
, modifié
il y a plus de 15 ans
par Ertaï
|
|
La suite des tutoriels sur les notions de base des Rubik's cubes.
Importance de la décomposition
De la même façon que tout nombre est décomposable en un produit de nombres premiers, tout puzzle du type Rubik ets décomposable en un produit de sous-puzzles de base. Ces sous-puzzles sont constitués des différents groupes de pièce.
Le dénombrement du nombre de permutation totales du puzzle oblige à identifier ces groupes de pièces et à comprendre leur comportement. Plus que le nombre brut c'est la formation de ce nombre qui renseigne sur la conception du puzzle.
Chaque sous-groupe autorise des échanges de pièces qu'on dénombre comme des permutations.
Chaque sous-groupe autorise éventuellement des orientations de pièces
Décomposition du Rubik's Revenge
Les arêtes :
- il y a un groupe de 24 arêtes, soit 24! permutations
- ces arêtes ne sont pas orientées
Les centres :
- il y a un groupe de 24 centres, soit 24! permutations
- ces centres ne sont pas orientées
- ces 24 centres ne sont pas tous distincts, sur chacune des 6 faces on peut permuter librement les 4 centres de même couleur, il faut donc diviser par 4!⁶
Les coins :
- il y a un groupe de 8 coins, soit 8! permutations
- ces coins ont 3 orientations distinctes, il faut donc multiplier par 3⁸
- l'orientation des coins n'est pas totalement libre, le dernier coin est orienté sous la contrainte des 7 premiers, il faut donc en fait multiplier par 3⁷ au lieu de 3⁸
Le cube est un solide à symétrie octaédrale, on peut le tourner de 24 façons différentes, il faut donc diviser par 24.
Total du Rubik's Revenge :
Citation :
"
24! (24! / 4!⁶) (8! 3⁷) / 24
"
Décomposition du Gigaminx
Avec le Gigaminx, on change de forme, on change de taille, le puzzle n'est pas seulement plus gros il gagne en diversité.
Il y a plus de sous-groupes car toutes les arêtes ne sont pas interchangeables et tous les centres ne sont pas interchangeables.
Les coins :
- il y a un groupe de 20 coins (en rouge), soit 20! permutations
- comme ces coins ont 3 orientations distinctes et que l'orientation du dernier coin n'est pas libre il faut multiplier par 3¹⁹
Les centres :
- il y a 12 grosses pièces centrales (en rose), mais elles sont immobiles comme les centres d'un cube 3³, donc pas de permutation
- il y a 60 centres-coins (en orange), soit 60! permutations, ces 60 centres ne sont pas tous distincts, sur chacune des 12 faces on peut permuter librement les 5 centres-coins de même couleur, il faut donc diviser par 5!¹²
- il y a 60 centres-arêtes (en violet), soit 60! permutations, ces 60 centres ne sont pas tous distincts, sur chacune des 12 faces on peut permuter librement les 5 centres-arêtes de même couleur, il faut donc diviser par 5!¹²
Les arêtes :
- il y a 60 arêtes-latérales (en bleu), soit 60! permutations, ces arêtes-latérales ne sont pas orientées
- il y a 30 arêtes-centrales (en mauve), soit 30! permutations, ces arêtes-centrales sont orientées comme les arêtes d'un cube 3³, c'est-à-dire 2 orientations possibles mais l'orientation de la dernière arêtes-centrale n'est pas libre, soit 2²⁹ permutations supplémentaires
Le dodécaèdre possède 60 symétries qui rendent le solide identique à lui-même, il faut donc diviser le total par 60.
Total du Gigaminx :
Citation :
"
(20! 3¹⁹) (60! / 5!¹²)² 60! (30! 2²⁹) / 60
"
Personne n'a encore marqué son appréciation pour cet article. Soyez le premier !
|
|
 Version d'archive
Version d'archive



![[FACEBOOK] Les amis du travail bien fait [FACEBOOK] Les amis du travail bien fait](/var/crypte/storage/images/media/images/vignette/vignette-question/30275-1-fre-FR/Vignette-Question_vignette_article.png)